Sampling with Polyominoes
Citation:
Victor Ostromoukhov, Sampling with Polyominoes, Proceedings of ACM SIGGRAPH 2007,
ACM Transactions on Graphics, 26(3), 2007.
Abstract:
We present a new general-purpose method for fast hierarchical
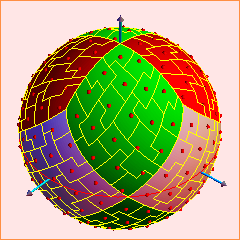
importance sampling with blue-noise properties. Our approach
is based on self-similar tiling of the plane or the surface
of a sphere with rectifiable polyominoes. Sampling points are
associated with polyominoes, one point per polyomino.
Each polyomino is recursively subdivided until the desired local
density of samples is reached. A numerical code generated during
the subdivision process is used for thresholding to accept or
reject the sample. The exact position of the sampling point within
the polyomino is determined according to a structural index, which
indicates the polyomino's local neighborhood. The variety of
structural indices and associated sampling point positions are
computed during the off-line optimization process, and tabulated.
Consequently, the sampling itself is extremely fast. The method
allows both deterministic and pseudo-non-deterministic sampling.
It can be successfully applied in a large variety of graphical
applications, where fast sampling with good spectral and visual
properties is required. The prime application is rendering.
Keywords:
Importance sampling, Blue noise, Polyominoes, Non-periodic tiling, Deterministic sampling.
On-line documents:
Complete article
[Acrobat pdf file, 7.7 Mb]
Companion Video
[WMV, 15.9 Mb]
Example code in C++
