Stability-Aware Simplification of Curve Networks
William Neveu¹, Ivan Puhachov¹, Bernard Thomaszewski², Mikhail Bessmeltsev¹
¹ Université de Montréal
² ETH Zürich
Abstract
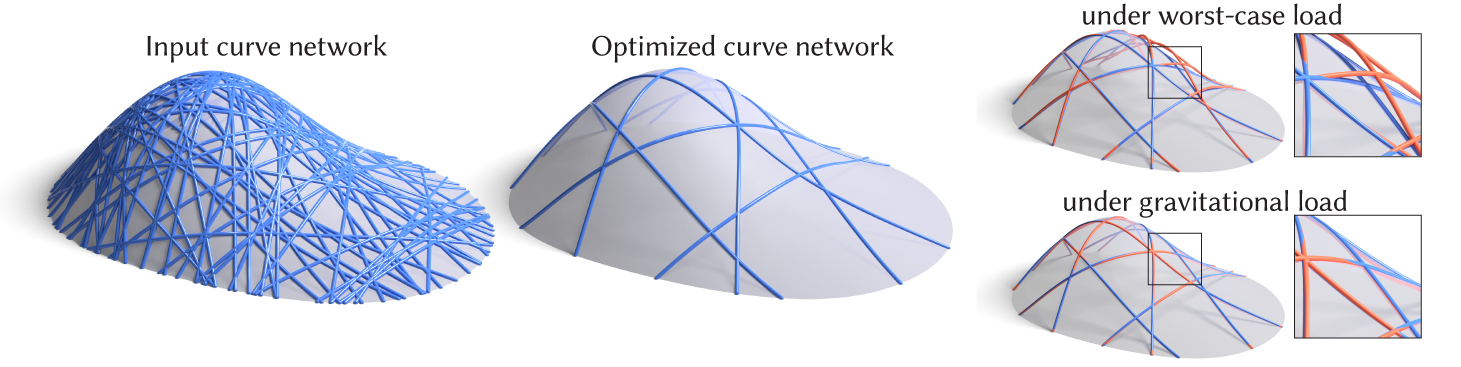
Designing curve networks for fabrication requires simultaneous consideration of structural stability, cost effectiveness, and visual appeal—complex, interrelated objectives that make manual design a difficult and tedious task.We present a novel method for fabrication-aware simplification of curve networks, algorithmically selecting a stable subset of given 3D curves. While traditionally stability is measured as magnitude of deformation induced by a set of pre-defined loads, predicting applied forces for common day objects can be challenging. Instead, we directly optimize for minimal deformation under the worst-case load.
Our technical contribution is a novel formulation of 3D curve network simplification for worst-case stability, leading to a mixed-integer semi-definite programming problem (MI-SDP). We show that while solving MI-SDP directly is infeasible, a physical insight suggests an efficient greedy approximation algorithm. We demonstrate the potential of our approach on a variety of curve network designs and validate its effectiveness compared to simpler alternatives using numerical experiments.
@inproceedings{Neveu:2022:curvenetworks,
author = {Neveu, William and Puhachov, Ivan and Thomaszewski, Bernhard and Bessmeltsev, Mikhail},
title = {Stability-Aware Simplification of Curve Networks},
year = {2022},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
booktitle = {ACM SIGGRAPH 2022 Conference Proceedings},
articleno = {20},
doi = {10.1145/3528233.3530711}
}
author = {Neveu, William and Puhachov, Ivan and Thomaszewski, Bernhard and Bessmeltsev, Mikhail},
title = {Stability-Aware Simplification of Curve Networks},
year = {2022},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
booktitle = {ACM SIGGRAPH 2022 Conference Proceedings},
articleno = {20},
doi = {10.1145/3528233.3530711}
}